■ 独立性の検定 事前の分析
独立性の検定は、クロス表の行と列との間に関連性がないことを帰無仮説として行う検定です。以下に示す2行3列のクロス表データを用いて説明をしていきます。
H1 対立仮説 (実際のデータ)
|
はい |
どちらでもない |
いいえ |
合計 |
| グルーブ1 |
10 |
30 |
20 |
60 |
| グループ2 |
30 |
20 |
10 |
60 |
| 合計 |
40 |
50 |
30 |
120 |
H0 帰無仮説
|
はい |
どちらでもない |
いいえ |
合計 |
| グルーブ1 |
20 |
25 |
15 |
60 |
| グループ2 |
20 |
25 |
15 |
60 |
| 合計 |
40 |
50 |
30 |
120 |
|
帰無仮説では、6個のセルの期待値(度数)を周辺度数の比率に基づいて算出する。例えば、グループ1の「はい」のセル、左上のセルの期待値は
(40/120)x(60/120)x 120 = 20 と計算する。実際の度数データは10だったのでズレがあることが分かる。
|
このデータのχ2値は 15.3333。そうしたχ2が得られる確率であるp値は 0.000468。したがって、0.1%水準でも有意なズレがあるといえるので、グループ1あるいはグループ2に属していることと、その被調査者たちの回答は独立ではなく関連しているといえる。
ということで、すでに分析を終えてしまったので、こうした結果の検定力の分析はこのコーナーの後半にある「事後の分析」で行います。
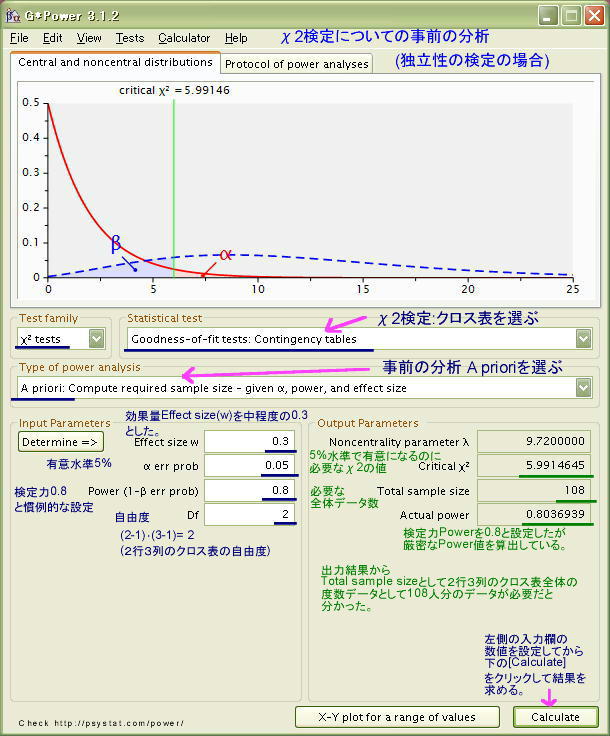
説明が前後してしまいましたが、こうした研究を実施する前にどの程度のデータ数が必要なのかについて、研究の設計という観点から「事前の分析」の仕方を説明しておきます。
G*Powerの画面の設定内容は、先に示した「適合度検定」の場合と同じです。
必要な数値を入力していき、{Calculate]で計算を実行すると、必要なデータ数が 108 と算出されました。この結果から、データ数は108を超える人数であれば良く、実際の研究では120人の被調査者を用いているので、データ数については妥当な研究計画となっていたことも確認できます。
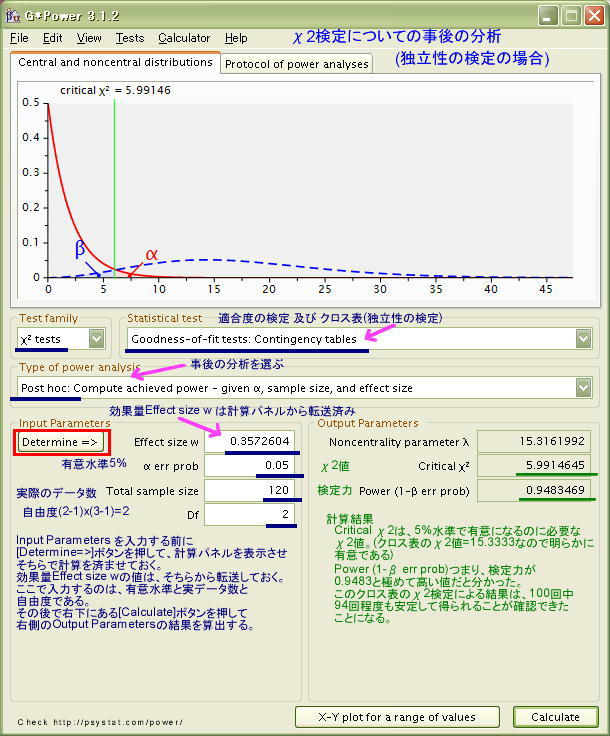
■ 独立性の検定 事後の分析
χ2検定による行と列との独立性の検定では、先に示した適合度検定の場合と異なりクロス表データが分析対象ですが、検定力分析の基本的な設定や内容は同じとなっています。以下のようにG*Powerの画面は適合度検定の場合と同じ設定項目で、異なるのは自由度(df:degree of freedom)の計算の仕方くらいです。
* 行数 r 列数 c とすると df=(r-1)x(c-1)です。
* 効果量の「大・中・小」(Large Medium Small)も同様で、ω=0.1 (効果量 小 Small)、 ω=0.3 (効果量 中 Medium)、 ω=0.5 (効果量 大 Large)、 となっています。
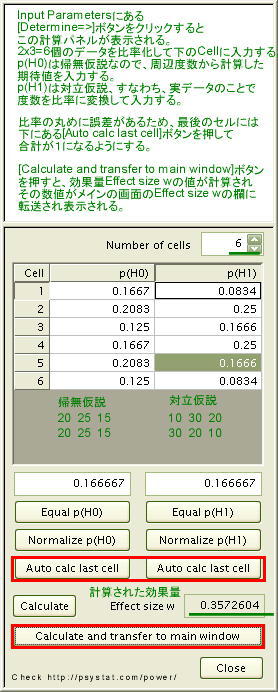
計算用のパネルはこの下に表示されます。
↓
クロス表データを比率化して入力して効果量を計算する。帰無仮説は、周辺度数から内部のセルの期待値を求め、それを比率化したものを入力します。これが p(H0)とされているものです。
対立仮説は実際の度数データであり、それを比率化して入力。これがp(H1)とされています。
研究後に「独立性のχ2検定」による結果がどの程度の検定力があるかを確認しています。
入力する必要があるのが、「α」「データ数」「効果量」の三つで、この3変数から「用いたχ2検定の検定力の大きさ」を見いだそうというわけです。実データから「効果量Effect size」が算出されるので、これを入力数値としてから、検定力を算出します。
得られた検定力 Powerは、0.94と極めて高いことが分かりました。すなわち、この研究を繰り返して実施したとして、そうした結果を100回中94回も安定して得られる可能性があることが確認できたのでした。
* 「赤い枠」で囲まれた部分をクリックすると、最下行の「説明欄」に簡単な説明が表示されます。
この部分を元に戻すときは、左側のフレームの下方にある「最下行の説明欄をクリア」をクリックしてください。
|
|
|