丂専掕椡丂
丂偙偺僐乕僫乕偱偼丄Jacob Cohen(1992)偺榑暥 "A Power Primer (専掕椡擖栧)" Psychological Bulletin, 1992, Vol.112, No.1, 155-159 傪嶲徠偟偮偮夝愢傪偟偰偄偒傑偡丅偙偺榑暥偵愭棫偮挊彂丄偡側傢偪1962擭偍傛傃1988擭偺戞2斉 亀Statistical power analysis for behavioral sciences (峴摦壢妛偺偨傔偺摑寁揑専掕椡暘愅)亁偼愱栧壠偵傛偭偰堷梡傗嶲徠偝傟丄専掕椡暘愅偺婎慴揑側暥專偲埵抲偯偗傜傟偰偄傑偡丅偟偐偟丄偦偺撪梕偼崅搙偵愱栧揑偱偁傞偨傔丄怱棟妛椞堟傪娷傫偱偦偺屻傕埶慠偲偟偰専掕椡暘愅偑媟岝傪梺傃偰偄側偄尰忬傪扱偄偰彂偐傟偨偺偑1992擭偺偙偺榑暥偱偡丅偦偺嵺丄榑暥曇廤幰偐傜丄摑寁偺愱栧壠偲偼尷傜側偄尋媶幰偵懳偟偰庤寉偵巊偊傞傕偺傪採嫙偟偰傒偰偼偲懀偝傟偨偲弎傋傜傟偰偄傑偡丅
丂偙偺榑暥偱偼丄専掕椡暘愅傪弰傞扱偐傢偟偄宱堒偵傆傟偨屻丄條乆側専掕曽朄偵偍偄偰峫椂偡傋偒乽岠壥検 (Effect Size) 乿丄偮傑傝丄梡偄傞専掕偑偳偺掱搙偺岠壥傪傕偭偰専掕傪偟偰偄傞偺偐傪敾掕偡傞偨傔偺巜昗 (ES index) 偑採帵偝傟丄娙扨側愢柧偑壛偊傜傟偰偄傑偡丅昞侾偵岠壥検偺巜昗乽ES index (Effect Size index)乿偑傑偲傔傜傟丄昞俀偵偼専掕朄枅偵乽昁梫側僨乕僞悢 (俶: sample size)乿偑採帵偝傟偰偄傑偡丅
丂
丂偙偙偱偼丄偙偺擇枃偺昞傪惓偟偔棟夝偡傞偙偲傪栚揑偲偟偰丄婎杮揑側梡岅偲峫偊曽偵偮偄偰愢柧傪壛偊偰偄偒傑偡偑丄桳堄惈専掕偵偮偄偰婎杮揑側棟夝偑偁傞偙偲傪慜採偲偟偰偄傑偡丅偙偙偱偺夝愢偼丄J.Cohen偵傛傞昞侾偲昞俀偵娭傢傞晹暘傪拞怱偵偟偰偄傞偺偱丄榑暥偺徻嵶偵偮偄偰偼尨揟偵捈愙摉偨偭偰捀偗傟偽偲巚偄傑偡丅(昞侾偲昞俀傪梡堄偟偰偔偩偝偄仺丂J.Cohen 1992 偺榑暥 "A Power Primer"偼偙偪傜"Cohen1992.pdf"偱偡丅(仼2/10, 2018: 榑暥偑撉傔傞傛偆偵偟傑偟偨)
丂丂
丂専掕椡暘愅偵搊応偡傞梡岅偼師偺捠傝偱偡丅
- 兛 (傾儖僼傽)丗丂桳堄悈弨偺妋棪抣丂0.05 (5%)偁傞偄偼丂0.01 (1%)傪梡偄傞偙偲偑懡偄丅
乽戞嘥庬偺岆傝 Type I error乿傑偨偼乽兛夁岆乿偺掱搙傪帵偡丂(兛偼0乣1)
- (婣柍壖愢偑惓偟偄偺偵岆偭偰婞媝偟偰偟傑偆妋棪)
- 兝 (儀乕僞)丗丂乽戞嘦庬偺岆傝 Type II error乿傑偨偼乽兝夁岆乿偺掱搙傪帵偡 (兝偼0乣1)
- (婣柍壖愢偑娫堘偭偰偄傞偺偵婞媝偟側偄偱偄傞妋棪丅傑偨偼丄懳棫壖愢偑惓偟偄偺偵嵦戰偟側偄偱偄傞妋棪)
- 侾亅兝 (侾儅僀僫僗 儀乕僞)丗丂専掕椡
- (懳棫壖愢傪惓偟偔嵦戰偡傞妋棪)
- 俤俽 (Effect Size)丗丂岠壥検
婣柍壖愢偲懳棫壖愢偲偺僘儗偺検偱丄偙傟偑戝偒偄傎偳岠壥検偑戝偒偄偲偄偆丅
- 俤俽 index丗丂岠壥検傪帵偡巜昗
t専掕傗冊2専掕丄暘嶶暘愅側偳偱偦傟偧傟偺岠壥検傪帵偡巜昗(寁嶼幃)偑堎側傞丅
- 俶 (sample size)丗丂昗杮偺戝偒偝丒僨乕僞悢偺偙偲
幚尡傗尋媶慜偵揔愗偱昁梫側僨乕僞悢傪妱傝弌偣傞偙偲偑嵟弶偺栚揑偲側傞丅
* 専掕椡暘愅偼乽兛丄 ES丄 俶丄1-兝丂乿偺巐偮偺梫慺偵傛偭偰峔惉偝傟丄偦偺偆偪偺堦偮偺巜昗偼巆傝偺嶰偮偺巜昗偺慻傒崌傢偣偵傛偭偰嶼弌偝傟傞偲偄偆娭學偵偁傝傑偡丅
昁梫側僨乕僞悢乽俶乿傪偁傜偐偠傔妱傝弌偡偨傔偵偼丄巆傝偺乽兛丄 ES丄 1-兝乿偺嶰偮偑寛傑傜側偄偲寁嶼偱偒傑偣傫丅兛偼5%傗1%偺桳堄悈弨側偺偱栤戣偁傝傑偣傫偑丄ES(岠壥検)偲 1-兝(専掕椡)傪掕傔側偗傟偽側傝傑偣傫丅J. Cohen偼 乽1-兝(専掕椡)乿傪巄掕揑偍傛傃姷椺揑偵乽0.8乿偲愝掕偟偰偄傑偡丅偦偟偰丄巆偭偨乽ES(岠壥検)乿傪夝愢偟偮偮丄昞侾偵採帵偟偰偄傞傢偗偱偡丅
丂拲丂堄丂丂J.Cohen(1992)偺悢昞(p.158)偵帵偝傟偰偄傞僨乕僞悢俶偼丄乽偦傟偧傟偺僌儖乕僾偺僨乕僞悢 (N as here defined is the necessary sample size for each group)乿(摨忋丄p.156)偲愢柧偝傟偰偄傑偡丅
偟偐偟丄冊2専掕偵偮偄偰挷傋偰傒傞偲丄J.Cohen(1988, 2nd Edition)偺杮偱偼丄悢昞偺悢抣偼乽昁梫側慡懱偺僒儞僾儖悢 The necessary total sample size N 乿(p.252)偲彂偐傟丄偦偺悢昞偺悢抣偼J.Cohen(1992)偺榑暥偲摨堦偺撪梕偲側偭偰偄傑偡丅偮傑傝丄冊2専掕偵偮偄偰偼丄偳偪傜偺悢昞傕 乽昁梫側慡搙悢傪帵偡乿 傕偺偲側偭偰偄傑偡丅
偙偆偄偆廳梫側偲偙傠偱僘儗偑偁偭偨偙偲偵嶰儢寧屻偺崱崰婥偑偮偄偨偲偙傠偱偡丅巐寧偐傜偺慜婜島媊側偳偵朲嶦偝傟偰偄偨偲偼偄偊丄戝曄偵怽偟栿偁傝傑偣傫丅偄傑偼慡懱傪尒捈偡帪娫偑偁傝傑偣傫偺偱丄偲傝偁偊偢丄冊2専掕偵偮偄偰偼乽悢昞(1992, p.158)偼慡搙悢傪帵偟偰偄傞乿偙偲傪巜揈偟偰偍偒傑偡丅
側偍丄G*Power僜僼僩偱偺僨乕僞悢偼婎杮揑偵乽慡僨乕僞悢 Total sample size乿偑昞帵偝傟傑偡丅偟偨偑偭偰丄J.Cohen偺1992擭偺悢昞傪梡偄傞応崌偼丄偹傫偺偨傔丄G*Power僜僼僩傪梡偄偰丄乽偦傟偧傟偺僌儖乕僾偺搙悢乿側偺偐乽慡搙悢乿側偺偐傪妋擣偟偰傕傜偊傟偽偲巚偄傑偡丅(6/25, 2011)
- 桳堄惈専掕偩偗偱偼側偔丄側偤乽専掕椡偺暘愅乿傪偡傞昁梫偑偁傞偺偐乗
- 媫偄偱偄傞恖偼偙偪傜偵偳偆偧仺 [専掕椡偺暘愅傪偟側偄偲偳偆側傞偺偐丠]
丂丂
- 僨乕僞悢偑嬌傔偰懡偄偲丄傎傫偺彮偟偺堘偄偱傕乽摑寁揑偵桳堄乿偲弌偰偟傑偆偙偲偑偁傞丅
偦偟偰乽摑寁揑偵桳堄乿偩偐傜偲偄偆崻嫆偱丄幚幙揑偵偼堄枴偑側偄夝庍偵娮傞応崌偑偁傞丅
- 僨乕僞悢偑彮側偄偲堦斒偵桳堄偵側傞壜擻惈偑掅偄丅偟偐偟乽桳堄偱偼側偄乿偲偄偆偙偲偑徹柧偝傟偨偺偱偼側偔P偵僨乕僞悢偑彮側偡偓偰乽専掕椡乿偑掅偄偨傔偵偦偆側偭偨壜擻惈偑偁傞丅
- 幚尡傗尋媶偵愭棫偭偰専掕椡傪妱傝偩偟偰揔愗側僨乕僞悢偱尋媶傪峴偆偙偲偑偱偒傞丅偦傟偵傛偭偰丄忋偺1)2)偺娫堘偄偺壜擻惈傪攔彍偡傞偙偲偑偱偒傞丅
丂丂
- 偮傑傝丄専掕椡暘愅傪峴偊偽専掕寢壥傪偳偺掱搙庡挘偟偰椙偄偺偐偑柧妋偲側傞偺偱丄寢壥偺夝庍偺濨枂偝傪尭傜偡偙偲偑偱偒傞丅偨偲偊偽乗
- 乽堦尒偟偰僨乕僞悢偑彮側偄偗傟偳傕専掕椡偑戝偒偄偺偱丄桳堄偲偄偆専掕寢壥傪嫮偔庡挘偟偰傕傛偄乿
- 乽僨乕僞悢偑彮側偔専掕椡偑彫偝偄偺偱丄桳堄偱偼側偄偲偄偆専掕寢壥偐傜壗傜偐偺夝庍傪恑傔偰偼側傜側偄乿
- 乽僨乕僞悢偑懡偔偰桳堄側寢壥傪摼偨偑丄幚幙揑側嵎偑彫偝偔専掕椡偑彫偝偄偺偱嫮偔庡挘偡傞崻嫆偲側傜側偄乿
- 乽僨乕僞悢偑懡偔偰桳堄側寢壥傪摼傞偲偲傕偵専掕椡偑戝偒偄偺偱丄桳堄偲偄偆寢壥傪嫮偔庡挘偟偰傕椙偄乿
- 乽婣柍壖愢偑婞媝偝傟側偐偭偨偲偄偆帠幚傪傕偭偰偨偲偊偽乽嵎偑側偄偙偲偑徹柧偝傟偨乿偲偄偭偨傛偆側庡挘偵偮偄偰丄専掕椡偑掅偗傟偽懨摉偱偼側偄偲敾抐偱偒傞乿側偳丅
- 岠壥検 (Effect Size) 偼丄婣柍壖愢偲懳棫壖愢偲偺僘儗偺搙崌偄偺戝偒偝傪帵偟偰偄傑偡丅
丂乽擇偮偺僌儖乕僾偺暯嬒抣偺嵎偺 倲 専掕乿傪椺偵偲偭偰傒傑偡丅僌儖乕僾倎偲僌儖乕僾倐偺暯嬒抣偑堘偭偰偄傞偐傪専掕偡傞偲偒丄師偺擇偮偺壖愢傪憐掕偟偰偄傑偡丅
婣柍壖愢俫0偼乽擇偮偺暯嬒抣偵偼嵎偑側偄乿偲偄偆傕偺偱偡丅
懳棫壖愢俫1偼乽擇偮偺暯嬒抣偼堎側傞乿偲偄偆傕偺偱偡丅
丂幚嵺偵挷傋偰傒傞偲偡偖偵暘偐傝傑偡偑丄擇偮偺僌儖乕僾偺暯嬒抣偑偒偭偪傝摍偟偔側傞偙偲偼柵懡偵偁傝傑偣傫丅偟偨偑偭偰丄偦偺嵎偑彮偟偺嵎側偺偐戝偒側嵎偑偁傞偺偐偑廳梫偲側傞傢偗偱偡偑丄偙偙偱偝傜偵栤戣偲側傞偺偑僨乕僞悢俶(sample size)偱偡丅僌儖乕僾倎丄倐 偲傕偵 5恖偢偮偩偲偟偰乽戝偒側嵎偑偁偭偨乿偲偟偰傕丄偦傟偼偦偺昗杮偑曃偭偰偄傞偩偗偱丄懠偺恖傪挷傋偨傜寢壥偼堎側偭偰偄偨偐傕偟傟傑偣傫丅偟偨偑偭偰丄偁傞掱搙偺恖悢傪挷傋側偄偲偄偗側偄偙偲偼尩枾側摑寁妛傪抦傜側偔偲傕悇應偑偮偔偲偙傠偱偡丅
丂偱偼壗恖偢偮挷傋傞偲椙偄偺偱偟傚偆偐丅幚嵺偼挷嵏偵偐偐傞庤娫壣偲旓梡側偳丄偦偆偟偨尰幚揑側惂栺偱壗恖掱搙傑偱挷傋傞偙偲偑偱偒傞偐偑寛傑偭偰偒傑偡丅偦傟傎偳庤娫壣偑偐偐傜側偄偺側傜偽丄僨乕僞悢偼懡偄偙偲偵墇偟偨偙偲偼偁傝傑偣傫丅偟偐偟庤娫壣傗僐僗僩偑偐偐傝夁偓偰僨乕僞悢傪憹傗偣側偄偲偒丄偦傟偱傕偳偺掱搙傑偱僨乕僞傪廤傔傞傋偒偱偟傚偆偐丠幚偼丄偙偆偟偨忬嫷偵偍偄偰丄専掕椡暘愅偑昁梫偲側偭偰偒傑偡丅
丂偙偙偱丄擇偮偺暯嬒抣偑戝偒偔堎側偭偰偄傞応崌(偦偺傛偆偵梊應偱偒傞応崌)偼丄僨乕僞悢偼偦傟傎偳懡偔側偔偲傕戝忎晇偦偆偱偡丅偮傑傝駛聜虄O儖乕僾丄倎偲倐偺暯嬒抣偺嵎偑戝偒偄偲偒偼僨乕僞悢偼偦傟傎偳偄傜側偄丅岠壥検偑戝偒偄偩傠偆偲梊應偝傟傞偐傜偱偡丅
丂偟偐偟丄暯嬒抣偑帡捠偭偰偄傞応崌偼岠壥検偑彫偝偄偩傠偆偐傜丄僨乕僞悢傪懡偔偲傜側偄偲桳堄側嵎偑弌偰偙側偄偲巚傢傟傑偡丅偮傑傝駛聜虝綃蠏l偺嵎偑彫偝偄偲偒偼僨乕僞悢偼偁傞掱搙昁梫偲側傞丄偲偄偆偙偲偱偡丅
丂偙偆偟偨揰傪墴偝偊側偑傜僨乕僞悢偑偳偺掱搙昁梫側偺偐傪尒偰傒傑偟傚偆丅
丂
- J.Cohen偺昞侾偺[Test 1] 偼 "倣倎 vs. 倣倐 for independent means"丂偱偁傝丄
(擇偮偺) 撈棫偟偨暯嬒抣偺懳斾丄偡側傢偪丄暯嬒抣偺嵎偺 倲 専掕傪巜偟偰偄傑偡丅
乽擇偮偺僌儖乕僾偺暯嬒抣偑戝偒偔堘偭偰偄傞応崌乿丄
- 偙傟傪乽岠壥検 (Effect Size) 偑戝 (Large)偲偄偆乿丂岠壥検倓亖0.8
乽擇偮偺僌儖乕僾偺暯嬒抣偑拞掱搙偵堎側偭偰偄傞応崌乿丄
- 偙傟傪乽岠壥検 (Effect Size) 偑拞 (Medium)偲偄偆乿丂岠壥検倓亖0.5
乽擇偮偺僌儖乕僾偺暯嬒抣偑偁傑傝堎側偭偰偄側偄応崌乿丄
- 偙傟傪乽岠壥検 (Effect Size) 偑彫 (Small)偲偄偆乿丂岠壥検倓亖0.2
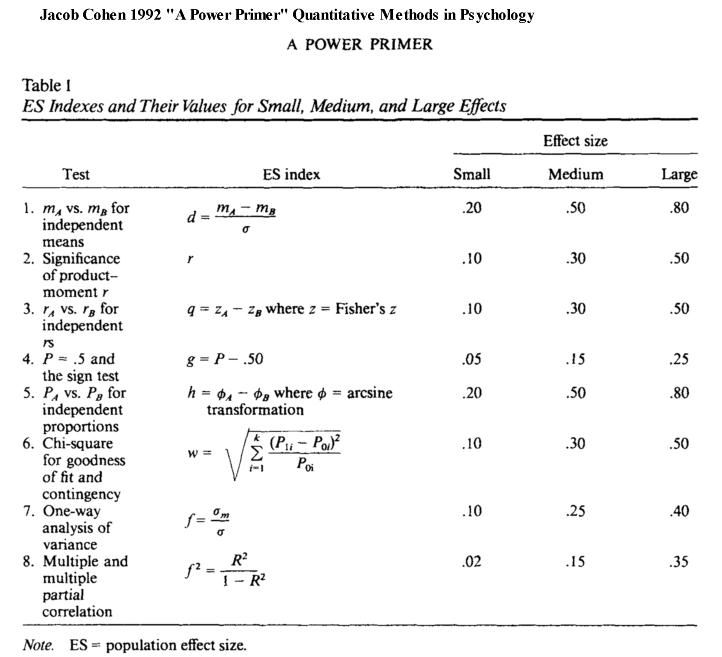
丂J.Cohen偼丄暘偐傝傗偡偄悢昞偲偟偰傑偲傔傞嵺偵丄岠壥検傪乽戝啣彫乿偲暘偗偰巊偄傗偡偄傛偆偵偟偰偄傑偡丅偙偙偱丄
乽彫 Small乿偺岠壥検偲偼丄乽堘偄偼彮側偄偗傟偳傕硤訓艂蛡葌鰮x偺嵎偑偁傞乿丅乽拞 Medium乿偺岠壥検偲偼丄乽尋媶幰偑拲堄怺偔僨乕僞傪尒傟偽偦傟偲暘偐傞傎偳綃蠏l偺嵎偑偦傟側傝偵擣幆偱偒傞乿傕偺丅乽戝 Large乿偺岠壥検偲偼丄乽柧傜偐偵嵎偑偁傞乿偲偟偰偄偰丄岠壥検倓偼丂0.2 0.5 0.8 偲摍娫妘偵埵抲偯偗傜傟偰偄傑偡丅偙偺暘偗曽偲岠壥検偺嶰偮偺悢抣偼丄乽椺偊偽偙偺偔傜偄乧乿偲偄偆堄枴偱乽姷椺 convention乿偲偝傟偰偄傑偡丅
暯嬒抣偺嵎偺 倲 専掕偱偼丄J.Cohen偵傛傞岠壥検倓偼師偺幃偱掕媊偝傟偰偄傑偡丅
- 岠壥検丂倓亖乮 倣倎 亅丂倣倐丂乯乛丂冃
偙偙偱倣倎偼僌儖乕僾倎偺暯嬒抣丄倣倐偼僌儖乕僾倐偺暯嬒抣丄冃(僔僌儅)偼昗弨曃嵎丅
偙偺幃偼丄擇偮偺僌儖乕僾偺暘晍偑偳偺掱搙偢傟偰偄傞偐偺巜昗偲側偭偰偄傑偡丅戝偒偔偢傟偰偄傞傎偳岠壥検偑戝偒偔側傝傑偡丅
- *側偍丄冃亖 併乮(冃倎俀 亄丂冃倐俀)/俀乯
* 戝曄偵偁傝偑偨偄偙偲偵専掕椡暘愅偺寁嶼傪帺摦偱偟偰偔傟傞僼儕乕僜僼僩(塸岅)偑採嫙偝傟偰偄傑偡丅G*Power 偲偄偆柤徧偱偡丅暿偺僐乕僫乕偱巊偄曽傪夝愢偟偰偄傞偺偱偦偪傜傪嶲峫偵偟偰偔偩偝偄丅
* G*Power偺寁嶼僜僼僩偼丄僴僀儞儕僢僸丒僴僀僱戝妛僨儏僢僙儖僪儖僼峑偺幚尡怱棟妛尋媶強 (Windows XP/Vista, Mac OS 7-9)偑採嫙偟偰偄傑偡丅杮摉偵彆偐傝傑偡偹 (^_^v
- J.Cohen偺昞俀偺[Test 1. Mean diff]偺侾峴偑丄 倲 専掕偱昁梫偲偝傟傞僨乕僞悢俶傪帵偟偰偄傑偡丅Table2偵偼師偺昞婰偑偁傝傑偡丅
乽N for Small, Medium, and Large ES乿偼乽岠壥検ES偑丂彫丒拞丒戝偱偁傞偲偒偵昁梫側僨乕僞悢俶乿
乽at Power= 0.8 乿偼丂乽専掕椡亖 0.8 偲偟偰乿丂(偮傑傝 1-兝亖0.8 )
乽for 兛= .01, .05, and .10 乿偼丂乽桳堄悈弨兛偑 0.01(1%), 0.05 (5%), 0.10 (10%) 偺応崌乿
偲偄偆堄枴偱偡丅
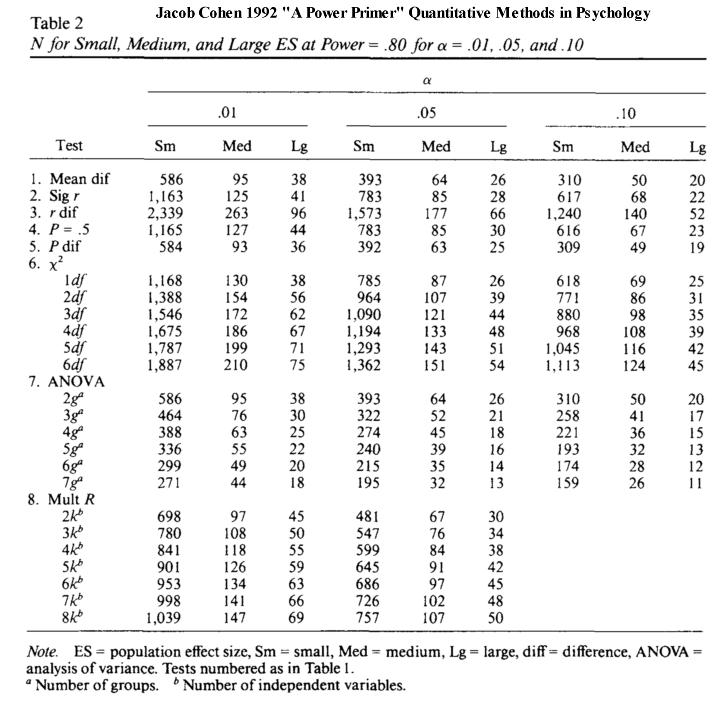
昁梫側僨乕僞悢 俶 偺昞丂(専掕椡 Power=0.8 偲愝掕)
拲 堄 J.Cohen偺悢昞偱偼丄昞帵偝傟偰偄傞僨乕僞悢偼偡傋偰乽堦偮偺僌儖乕僾偺僨乕僞悢乿偱偡丅(J.Cohen, 1992, p.156)
偟偨偑偭偰丄乽擇偮偺僌儖乕僾偺暯嬒抣偺嵎偺倲専掕乿偱昁梫偲偝傟傞慡僨乕僞悢偼丄
壓婰偺昞偺悢抣傪擇攞偵偡傞昁梫偑偁傝傑偡丅
| 桳堄悈弨仺 |
兛亖 0.01 |
兛亖 0.05 |
兛亖 0.10 |
| Effect Size 仺 |
丂Small |
丂Medium |
丂Large |
丂Small |
丂Medium |
丂Large |
丂Small |
丂Medium |
丂Large |
1. Mean diff丂
(暯嬒抣偺嵎偺 t 専掕) |
586 |
95 |
38 |
393 |
64 |
26 |
310 |
50 |
20 |
* J. Cohen (1992)偐傜偺堷梡丅
J.Cohen偺Table 2偼丄専掕椡 傪乽0.8乿偵愝掕偟偨(Power亖 0.8 )偲偒偺悢昞偲側偭偰偄傑偡丅偡側傢偪丄(1-兝)= 0.8 丅専掕椡偼乽0.00乣1.00乿偺悢抣偱丄戝偒偄傎偳専掕椡偑偁傝彫偝偄偲専掕椡偑側偄偙偲傪堄枴偟傑偡丅J. Cohen偼乽専掕椡偼0.8掱搙偑昁梫偱偁傞乿偲峫偊丄偙傟傕乽姷椺convention乿偲偟偰採帵偟偰偄傞傢偗偱偡丅専掕椡(1-兝)偑 0.8 傛傝傕彫偝偄偲丄戞擇庬偺岆傝(兝)偺妋棪偑崅偔側傝偡偓傞偙偲丄傑偨専掕椡(1-兝)偑0.8 傛傝傕崅偄偲偦傟傪幚尰偡傞偨傔偵昁梫偲偝傟傞僨乕僞悢俶偑戝偒偔側傝夁偓偰幚嵺揑偱側偔側傞壜擻惈偑偁傞偙偲丄J.Cohen偼偙偺擇偮偵攝椂偟偰乽 0.8 乿偲偄偆悢抣傪乽姷椺乿偲偟偰採彞偟偰偄傑偡丅
側偍丄乽専掕椡(1-兝)偑 0.8 乿偲偄偆偙偲偼丄乽戞擇庬偺岆傝乿乽兝夁岆乿(乽暯嬒抣偵偼嵎偑偁傞偲偄偆懳棫壖愢乿偑惓偟偄偺偵偄偮傑偱傕嵦戰偟側偄偱偄傞岆傝偺妋棪兝)偑乽兝亖 0.2 乿( 20%)偲偄偆偙偲偱偡丅偟偨偑偭偰丄娙扨偵尵偊偽乽 80%偺妋棪偱丄懳棫壖愢傪惓偟偔嵦戰偟偰偄傞乿偙偲傪帵偟傑偡丅
専掕椡偲偼乧丅
偙傟傑偱偼丄専掕傪偟偨寢壥乽5%偱桳堄偵側偭偨乿偲偐乽1%偱偼桳堄偱偼側偐偭偨乿偲偄偭偨偙偲偩偗傪栤戣偵偟偰偄傑偟偨丅偟偐偟丄偙偆偟偨専掕寢壥傪偳偺掱搙嫮偔庡挘偟偰傛偄偺偐偼丄偙偺専掕椡偺戝偒偝偵埶懚偡傞偺偱偡丅
丂偦偺偨傔丄乽5%偱桳堄乿偲偄偆寢壥傪摼偨偲偟偰傕丄壖偵乽専掕椡 Power= 0.3 乿偩偭偨側傜偽 (偡側傢偪兝亖 0.7 )丄乽5%偱桳堄偩偭偨偑丄偙偆偟偨寢壥偼30%偺妋棪偱摼傜傟傞偵夁偓側偄丅椺偊偰偄偆側傜偽丄偙偆偟偨幚尡傪100夞孞傝曉偟偰峴偆偲丄偦偺偆偪30夞偼亙桳堄亜偲偄偆寢壥偵側傞偑丄100拞70夞偼亙桳堄偱偼側偄亜偲偄偆寢壥偲側傞壜擻惈偑偁傞乿乧丅
丂偮傑傝丄偙傟傑偱偼乽桳堄偩偭偨乿偲戝婌傃偟偰敪昞偟偰偄偨偺偱偡偑丄幚偼偦傫側偵娙扨側榖偱偼側偐偭偨偺偱偡丅怱棟妛偼偙傟傑偱桳堄惈専掕傪偁偑傔曭偭偰偒偨偺偱偡偑丄尩枾偵尒偰傒傞偲堄奜偵傕掙偑敳偗偨傑傑偩偭偨乧丅J. Cohen偑50擭埲忋傕扱偒懕偗偰偄傞偺傕擺摼偱偒傑偡丅椺偊偰傒傟偽丄杮摉偼椉椫(兛夁岆偲兝夁岆)偑偁傞偺偵曅懁偺幵椫(兛夁岆)偩偗偱憱偭偰偄偨乧偲偄偆偐丅
仏拲堄
丂僨乕僞悢偑彮側偄拞偱桳堄偲側偭偨尋媶偱偼丄寢壥揑偵専掕椡偑崅偐偭偨偲偄偆応崌偑懡偔偁傝傑偡丅傑偨丄僨乕僞悢傪廫擇暘偵懙偊偨尋媶偼寢壥揑偵専掕椡偑崅偐偭偨応崌偑峫偊傜傟傑偡丅偟偨偑偭偰丄専掕椡暘愅傪峴偭偰偄側偄夁嫀偺尋媶榑暥偑偡傋偰傾僂僩偲偄偆栿偱偼偁傝傑偣傫丅朙揷廏庽亀専掕椡暘愅擖栧亁偱偼丄専掕椡偺帠屻暘愅傪峴偭偰偄傑偡丅寢壥揑偵懨摉偲偄偊傞尋媶椺傪拞怱偵採帵偝傟偰偍傝嶲峫偵側傝傑偡丅
乽暯嬒抣偺嵎偺 t 専掕乿偺応崌丄擇偮偺暯嬒抣偑戝偒偔堎側偭偰偄傞応崌偼丄帠屻偺専掕椡暘愅偵傛偭偰傕廫暘側専掕椡傪旛偊偰偄傞椺側偳偑帵偝傟偰偄傑偡丅
丂専掕椡暘愅偺寢壥傪偳偺傛偆偵昞婰偡傞偐丠丂
- 幚嵺偵僨乕僞傪摼偰偐傜峴偆乽帠屻偺専掕椡暘愅乿偺寢壥丄乽専掕椡丂Power(1-兝)=0.8765 乿偩偭偨偲偟傑偡丅偙偺悢抣偑寁嶼偝傟傞夁掱偱丄乽岠壥検 倓=0.5432乿偩偭偨偲偟傑偡丅側偍丄岠壥検傪帵偡巜昗 (Effect size index)偼丄専掕曽朄偵傛偭偰堎側傝傑偡丅倲 専掕偺応崌丄J. Cohen偺岠壥検巜昗倓傪梡偄偰偄傑偡偑丄冊2専掕偺応崌偺岠壥検巜昗偼丄J.Cohen偵傛傞巜昗偼冎偲側偭偰偄傑偡丅(偦傟偧傟偺巜昗偱帵偝傟傞岠壥検偺寁嶼幃偑堎側傞偨傔偱偡丅徻嵶偼J.Cohen(1992)傪嶲徠偺偙偲丅)
偟偨偑偭偰丄椺偊偽偙傫側姶偠偺彂偒曽偵側傞偱偟傚偆乗乽倲 専掕偵傛傞岠壥検偼倓=0.5432丄専掕椡偼0.8765偩偭偨乿偲偐丄乽倲 専掕偱偼丄J.Cohen偺帵偡戝偒側岠壥検(Large)偺0.5傪忋夞傞倓=0.5432偲側傝丄専掕椡偼0.8765偲廫暘偵戝偒偐偭偨乿摍乆丅
側偍丄暥枛偵抂揑偵帵偡応崌偼乽乧偱偁偭偨 (Effect size:倓=0.5432丄(1-兝)=0.8765)丅乿摍乆丅
偟偨偑偭偰丄廬棃偺桳堄惈専掕偲堦弿偵昞婰偡傞偲偒偼乽乧偱偁偭偨 (倲=2.468丄 p亙0.05丄ES: 倓=0.6000丄1-兝=0.6455)丅乿
偁傞偄偼乽乧偱偁偭偨 (冊2=12.3456丄 p亙0.01丄ES:冎=0.5432丄1-兝=0.8765)丅乿偲偄偭偨姶偠偱偟傚偆偐丅
偄偢傟偵偟偰傕丄乽丂帠丂屻丂偺専掕椡暘愅乿偵偮偄偰偼
丒岠壥検(Effect size)傪岠壥検巜昗(Effect side index)偺婰崋侾暥帤(倓丄冎丄乧)傪梡偄偰乽倓亖乧乧乿側偳偲帵偡偙偲丅
丒専掕椡(power)傪 乽侾亅兝亖乧乧乿偺宍側偳偱帵偡偙偲丄偙偺俀偮偺昞帵偑昁梫偲側傝傑偡丅
丂専掕椡丂乽侾亅兝乿偲偼丂
- 偙偙傑偱偺夝愢偼丄尋媶偵愭棫偭偰偳偺掱搙偺僨乕僞悢傪懙偊偨傜傛偄偐偲偄偆帇揰偱弎傋偰偒傑偟偨丅偙偙偱偼丄専掕椡偺杮懱乽1-兝乿偲偼偳偆偄偆偙偲傪堄枴偟偰偄傞偐丄彮偟徻偟偔夝愢偟偰偄偒傑偡丅摿偵乧
乽戞堦庬偺岆傝 Type I丂僄儔乕乿乽兛夁岆乿偲懳斾偟偰
乽戞擇庬偺岆傝 Type II丂僄儔乕乿乽兝夁岆乿偵偮偄偰夝愢偟傑偡丅
- 兛丗婣柍壖愢偑惓偟偄偺偵岆偭偰婞媝偟偰偟傑偆妋棪
- 兝丗婣柍壖愢偑娫堘偭偰偄傞偺偵婞媝偟側偄偱偄傞妋棪丅傑偨偼丄懳棫壖愢偑惓偟偄偺偵嵦戰偟側偄偱偄傞妋棪
- 侾亅兝丗丂専掕椡乽侾亅兝乿偲偼乽惓偟偄懳棫壖愢傪嵦戰偡傞妋棪乿傪巜偟傑偡丅
偙偙偱婎杮揑側偙偲偼乽兛偑1亅兝偵側傞偲偼尷傜側偄乿偲偄偆偙偲偱偡丅偮傑傝丄兛偲兝偼捈愙寢傃偮偄偰偄側偄偨傔偵丄偦傟偧傟屄暿偺懳墳傪偟側偗傟偽偄偗側偄偲偄偆偙偲側偺偱偡丅偙傟傑偱偼兛偺傒偵婥傪偲傜傟偰偄偨偗傟偳傕丄偦傟偱偼晄廫暘側偺偱偟偨丅
偙偙偱傑偨乽暯嬒抣偺嵎偺t専掕乿傪椺偵偲偭偰愢柧傪偟傑偡丅桳堄悈弨偲偟偰抦傜傟偰偄傞兛亖0.05 , 兛亖0.01 偲偼丄乽婣柍壖愢傪岆偭偰婞媝偡傞妋棪乿偱偡偑丄偦傟偑0.05 偲偐0.01 偲偐偲彫偝偄偺偱(5 %, 1 %)丄偦偆偟偨儕僗僋傪朻偟側偑傜婣柍壖愢傪婞媝偡傞傢偗偱偡丅偮傑傝丄乽擇偮偺暯嬒抣偼摨偠偲偼尵偊側偄乿偲偄偆偙偲偑丄95%偁傞偄偼99%偺妋棪偱庡挘偱偒傞偲偟偰偄傞偺偱偡丅
- 婣柍壖愢俫0偼乽擇偮偺暯嬒抣偵偼嵎偑側偄乿偲偄偆傕偺偱偡丅
- 懳棫壖愢俫1偼乽擇偮偺暯嬒抣偼堎側傞乿偲偄偆傕偺偱偡丅
桳堄惈専掕偺棟孅偲偟偰偼丄乽僌儖乕僾倎偺暯嬒抣偲僌儖乕僾倐偺暯嬒抣偑摨偠偩偲壖掕偟偰寁嶼偟偰傒傞偲丄偦傫側偵偢傟偨暯嬒抣偑嬼慠摼傜傟傞妋棪偼0.05 偁傞偄偼0.01 偟偐側偄乿偲幚嵺偵寁嶼偑壜擻偱偡 丅偝偰丄偦偆偄偆偙偲偩偭偨傜丄暯嬒抣偑摨偠偩偭偨偲偟偨憐掕偑偍偐偟偄丅偟偨偑偭偰丄0.05 偲偐0.01 偲偐偺兛夁岆偺妋棪傪娷傒側偑傜傕丄婣柍壖愢傪斲掕偟偰乽擇偮偺僌儖乕僾偺暯嬒抣偼堎側偭偰偄傞乿偲偄偆懳棫壖愢傪嵦戰偡傞丄偲偄偆嬝彂偒偱偡丅
* 嬶懱揑側悢抣偑梌偊傜傟傞偺偱丄摿掕偺暘晍偺尦偱偦偆偟偨偙偲偑偳偺掱搙婲偒傞偐傪偒偭偪傝嶼弌偱偒傞偺偱偡丅
丂偝偰丄懳棫壖愢乽擇偮偺僌儖乕僾偺暯嬒抣偼堎側傞乿偲偄偆壖愢傪嵦戰偡傞偺偼偄偄偺偱偡偑丄偱傕堦懱慡懱偳偺偔傜偄偢傟偰偄傞偺偱偟傚偆偐丠 僌儖乕僾倎偲僌儖乕僾倐偺恎挿嵎偩偲偟偰丄偦傟偼暯嬒抣偱1-2 僙儞僠偺偢傟側偺偐10悢僙儞僠偺偢傟側偺偐乧丅尋媶傪巒傔偨偽偐傝側傜偽丄偦偺偙偲偼傑偩暘偐偭偰偄傑偣傫偐傜帺怣傪帩偭偰庡挘偱偒傞悢帤偼尒摉偨傝傑偣傫丅偮傑傝丄懳棫壖愢偵偍偄偰偼丄偁傜偐偠傔偳偺掱搙偺僘儗偑偁傞偲偄偆柧妋側愝掕偑偱偒側偄偺偱丄堦偮偺悢抣偩偗傪偒偭偪傝偲採帵偡傞偙偲偑偱偒傑偣傫丅偮傑傝丄懳棫壖愢偼乽嵎偑偁傞乿偲拪徾揑偵尵偆偩偗偱丄偦傟偑偳偺掱搙偺嵎側偺偐傪嬶懱揑偵庡挘偟偰偼偄側偄偺偱偡丅偙偺偙偲偼乽婣柍壖愢偑惓偟偄偺偵岆偭偰婞媝偟偰偟傑偆妋棪乿兛夁岆偲偄偆僥乕儅偲偼丄捈愙揑偵寢傃偮偄偰偄側偄偙偲偑柧傜偐偱偡丅
* 戞堦庬偺岆傝偺妋棪兛偼丄婣柍壖愢偑惉傝棫偭偰偄傞偲偡傞慜採偺尦偱偄傢備傞乽 倫抣 乿傪嶼弌偟偰懳斾偝傟傞偺偵懳偟偰丄戞擇庬偺岆傝偺妋棪兝偼丄懳棫壖愢偑惉傝棫偭偰偄傞偲偡傞慜採偺尦偱婣柍壖愢傪婞媝偟側偄妋棪傪寁嶼偟偰偄傑偡丅偙偺傛偆偵寁嶼偦偺傕偺偺撪梕偑堎側偭偰偄傑偡丅
丂
丂専掕椡傪恾偱尒傞丂
- 専掕椡暘愅偲偼丄娙扨偵尵偆偲丄偙傟傑偱峴傢傟偰偙側偐偭偨乽兝夁岆乿偺栤戣傪偒偪傫偲庢傝埖偆偲偄偆偙偲偱偡丅廬棃偼桳堄悈弨 5%傗 1%偲偟偰傛偔抦傜傟偰偄傞乽兛夁岆乿偩偗偵拲栚偟偰丄乽兝夁岆乿偵偮偄偰偺埖偄偑側偍偞傝偵側偭偰偄偨偺偱偟偨丅埲壓偱偼丄乽暯嬒抣偺嵎偺t専掕乿偵偍偗傞t 暘晍傪恾帵偟偰丄兛夁岆偲兝夁岆偑偳偆偄偆峔憿傪偟偰偄傞偐傪尒偰偄偒傑偡丅
丒乽暯嬒抣偺嵎偺t専掕乿擇偮偺撈棫偟偨僌儖乕僾G1,G2丗僌儖乕僾撪偺僨乕僞悢偼50,50偲摨堦丅
丒桳堄悈弨丗兛亖0.05 (5%)
丒椉懁専掕丗偙偺偨傔倲暘晍偺椉懁偺偦傟偧傟2.5%偢偮偑婞媝堟偲側傞丅
丂椉懁専掕偲偼丄懳棫壖愢乽俀僌儖乕僾偺暯嬒抣偼堎側偭偰偄傞乿偲愝掕偟偰偄傞丅
丂曅懁専掕偲偡傞偲乽G1偺暯嬒抣偼G2傛傝傕戝偒偄(傑偨偼彫偝偄)乿偲憐掕丅
丒岠壥検丗彫(Small)=0.2丄拞(Medium)=0.5丄戝(Large)=0.8偺嶰偮傪憐掕偟偨丅
丂偦傟偧傟偺岠壥検偼丄擇偮偺僌儖乕僾偺暯嬒抣偺僘儗偑(彫啣戝)偲愝掕偟偰偄傞丅
愒偄慄偱昤偐傟偰偄傞偺偑倲暘晍偱偁傝丄兛/2丄偡側傢偪倲暘晍偺塃懁媦傃嵍懁偺偡偦栰偱丄偦傟傛傝奜懁偺柺愊偑乽0.025乿偲側傞屄強偑椢偺慄偱嬫愗傜傟偰偄傑偡丅
廬棃偼偙偺乽椉懁偺愒偄柺愊(兛/2)乿偩偗傪埖偭偰偄偨偺偱偡偑丄乽兝夁岆乿偡側傢偪乽懳棫壖愢傪嵦戰偟側偄岆傝乿傪帵偡乽惵偄柺愊乿偲偺寭偹崌偄傪峫椂偡傞偺偑専掕椡暘愅側偺偱偡丅側偍丄専掕椡Power偺戝偒偝傪帵偡妋棪(1-兝)偼丄兝偺斀懳懁偵偁傝丄乽(侾亅兝)懁偺柺愊乿偱帵偝傟偰偄傑偡丅
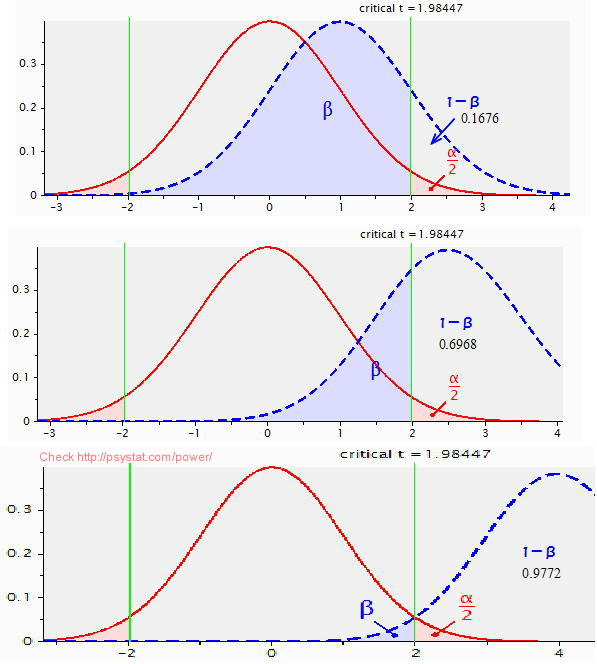 |
岠壥検=0.2 偲乽彫乿偺偲偒丄兝偺暘晍偑廳側偭偰偍傝丄専掕椡(1-兝)=0.1676偲嬌傔偰彫偝偄丅 |
| 岠壥検=0.5 偲乽拞乿偺偲偒丄兝偺暘晍偺廳側傝偑彮側偔側傝丄専掕椡(1-兝)=0.6968偲偐側傝戝偒偄丅 |
| 岠壥検=0.8 偲乽戝乿偺偲偒丄兝偺暘晍偺廳側傝偑嬌傔偰彫偝偔丄専掕椡(1-兝)=0.9772 偲戝偒偔丄兝夁岆偺妋棪偼0.0228偲彫偝偄丅 |
* 偙偺恾偼G*Power偺暘晍昞帵婡擻傪梡偄偰嶌惉偟傑偟偨丅
(曇廤拞乧)
丂
丂 |



